DS010:順列や組合せの式 nPr, nCr を理解し、適切に使い分けることができる
順列と組合せの違いを理解し、適切に使い分ける
「順列と組合せの違いが分からない」「どんな場面で使うのか知りたい」と思っていませんか?
日常生活や試験問題では、物の並べ方や選び方を考える機会が多くあります。たとえば、
- スポーツ大会で表彰台に立つ選手の並び方
- 抽選でランダムに3人を選ぶ方法
- パスワードの組み合わせの計算
このような場面で「順列(Permutation)」と「組合せ(Combination)」を適切に使い分けることが重要です。本記事では、それぞれの概念と計算方法を分かりやすく解説します。
順列(Permutation)とは?
順列とは「並べる方法」のことです。順番が重要な場合に使用します。
例えば、5人の中から3人を選び、順位をつけて並べる場合を考えましょう。
順列の公式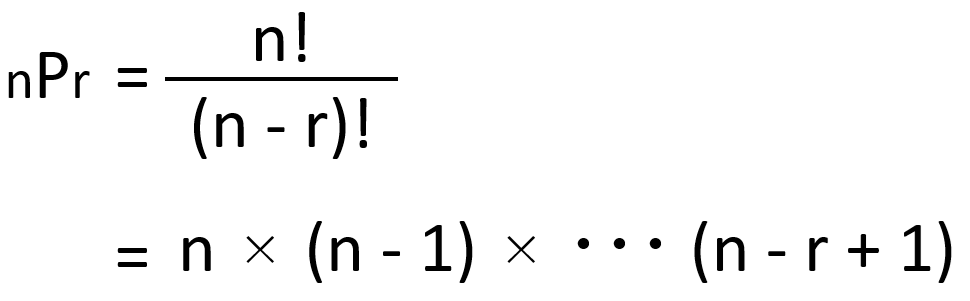
n:は全体の数 r:選ぶ数 !:階乗
例題:5人から3人を選んで並べる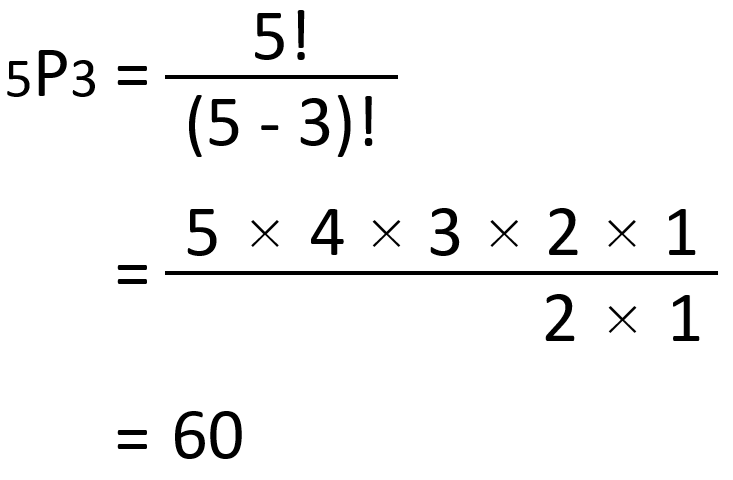
つまり、60通りの並べ方があることが分かります。
順列が使われる例
・競技大会の金・銀・銅メダルの並び順
・パスワードの生成(文字や数字の並びが異なると別のパスワードになる)
・席の並び順を決める
組合せ(Combination)とは?
組合せとは「選ぶ方法」のことです。順番を気にしない場合に使用します。
例えば、5人の中から3人を選ぶ場合、選ばれた3人の順番は関係ありません。
組合せの公式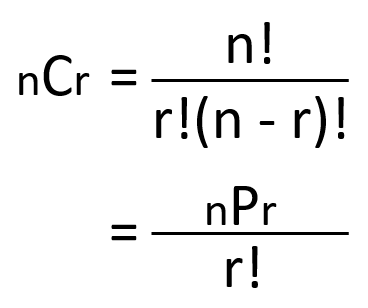
例題:5人から順番を気にせず3人を選ぶ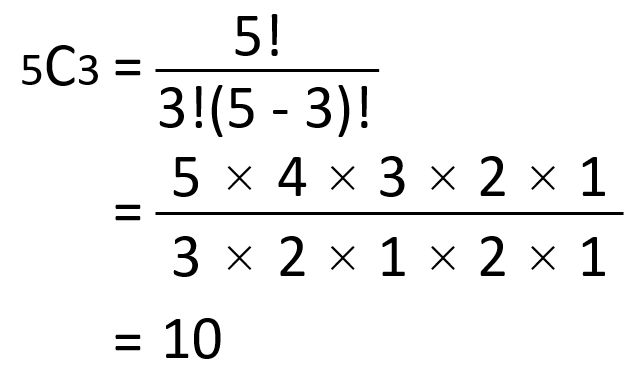
つまり、10通りの選び方があることが分かります。
組合せが使われる例
・抽選で3人を選ぶ(順番は関係なし)
・サークルのメンバーを3人選ぶ
・宝くじの数字の選び方
順列と組合せの違いのまとめ
| 順列(Permutation) | 組合せ(Combination) | |
|---|---|---|
| 定義 | 並べ方を考える(順番が重要) | 選び方を考える(順番は関係なし) |
| 公式 | nPr = n! ÷ (n−r)! | nCr = n! ÷ r!(n−r)! |
| 例 | 競技の順位決め、席の並び順 | 抽選、グループ選び |
どちらを使うべきか?
迷ったら「順番を考えるかどうか」を意識しましょう。
✅ 順番を考えるなら順列(Permutation)
✅ 順番を気にしないなら組合せ(Combination)
たとえば、
- 「Aさん・Bさん・Cさん」と「Cさん・Aさん・Bさん」を別扱い → 順列
- 「Aさん・Bさん・Cさん」と「Cさん・Aさん・Bさん」を同じ扱い → 組合せ
この違いを押さえておけば、問題を解くときに迷わず使い分けができます。
まとめ
- 順列は順番を考える並べ方、組合せは順番を考えない選び方
- 公式を理解し、使い分けることで計算がスムーズに
- 実生活や試験問題でも活用できる知識
順列・組合せは数学やデータ分析、さらには日常生活にも関わる重要な概念です。しっかり理解し、実践で使いこなしていきましょう!



コメント