DS008:和集合、積集合、差集合、対称差集合、補集合についてベン図を用いて説明できる
はじめに
集合の概念は、数学や情報科学において重要な役割を果たします。特に、データ処理やプログラミングでは、集合の関係を正しく理解することで、効率的なデータ操作が可能になります。
この記事では、ベン図を用いて 和集合、積集合、差集合、対称差集合、補集合 の概念をわかりやすく解説します。集合の基本を押さえておくことで、検索クエリの最適化やデータ分析にも役立ちます。
ベン図とは?
ベン図は、集合の関係を視覚的に表現する図 です。円や楕円で集合を表し、それらの重なりや外側の領域が集合間の関係を示します。
例えば、あるグループAとグループBがあった場合、それらの共通メンバーや片方にしか属さないメンバーをベン図で簡単に表現できます。
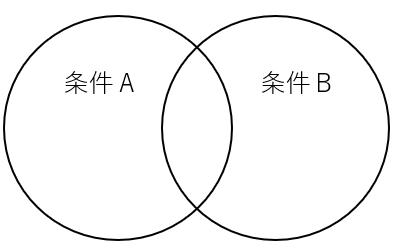
集合の基本概念とベン図
和集合(Union)
和集合 とは、2つの集合のいずれか、または両方に含まれる要素の集合 です。
記号表記: A ∪ B(または A | B)
ベン図の特徴 : AとBの円全体が該当(重なった部分も含む)
- 「数学が得意な生徒(A)」と「英語が得意な生徒(B)」の和集合 → どちらかが得意な生徒全員
- SQLで
SELECT * FROM Table1 UNION SELECT * FROM Table2のように全データを結合
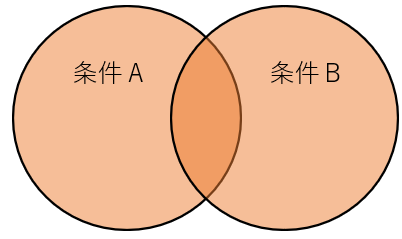
積集合(Intersection)
積集合 とは、2つの集合の両方に共通する要素の集合 です。
記号表記 : A ∩ B(または A & B)
ベン図の特徴 : AとBの円が重なっている部分のみ
- 「数学が得意な生徒(A)」かつ「英語が得意な生徒(B)」の積集合 → 両方が得意な生徒のみ
- SQLで
SELECT * FROM Table1 INNER JOIN Table2に相当
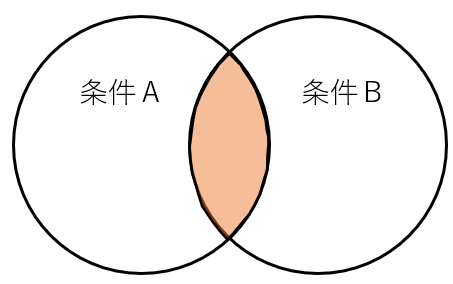
差集合(Difference)
差集合 とは、Aに含まれるが、Bには含まれない要素の集合 です。
記号表記 : A \ B(または A – B)
ベン図の特徴 : Aの円のうちBと重ならない部分のみ
- 「数学が得意な生徒(A)」で、「英語は得意ではない生徒」
- SQLで
SELECT * FROM Table1 WHERE NOT EXISTS (SELECT * FROM Table2 WHERE Table1.id = Table2.id)
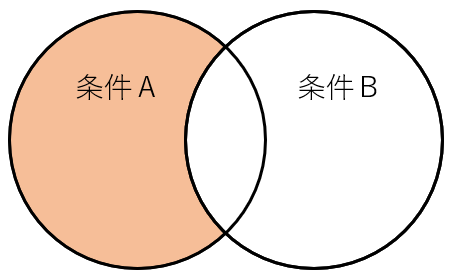
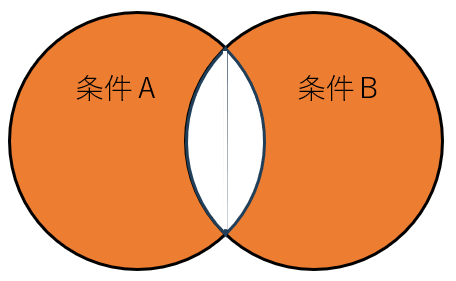
対称差集合(Symmetric Difference)
対称差集合 とは、どちらか一方にだけ属する要素の集合 です(共通部分は除く)。
記号表記 : A △ B(または A ^ B)
ベン図の特徴 : AとBのうち、共通部分を除いた部分が該当
- 「数学のみ得意な生徒」または「英語のみ得意な生徒」
- SQLで
SELECT * FROM (Table1 EXCEPT Table2) UNION (Table2 EXCEPT Table1)
補集合(Complement)
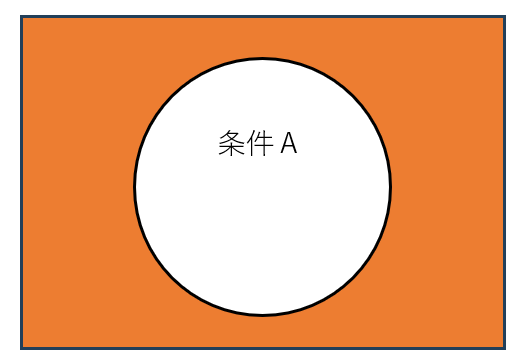
補集合 とは、全体集合(U)のうち、Aに含まれない要素の集合 です。
記号表記 : Aᶜ(または Ā)
ベン図の特徴 : Aの外側の部分が該当
- 「数学が得意ではない生徒」
- SQLで
SELECT * FROM Students WHERE NOT EXISTS (SELECT * FROM Math_Students WHERE Students.id = Math_Students.id)
まとめ
集合の概念は、日常生活からデータ分析、プログラミングまで幅広く活用されます。ベン図を活用することで、集合の関係が直感的に理解しやすくなります。
今回紹介した 和集合、積集合、差集合、対称差集合、補集合 を理解することで、データのフィルタリングや条件分岐を効率的に設計する力が身につきます。
実際に、データ分析やSQLクエリ作成の際に、これらの集合操作を意識してみてください!


コメント