DS012:平均、中央値、最頻値の算出方法の違いを説明できる
本記事で解決できる課題
データ分析をする際、データの特徴を表す「代表値」を適切に選ぶことが重要です。しかし、
- 平均・中央値・最頻値の違いがよくわからない
- どの代表値を使えばよいのか判断に迷う
- 実際の活用例を知りたい
といった悩みを抱える方も多いでしょう。本記事では、代表値の意味や算出方法、それぞれの特徴と活用シーンについて詳しく解説します。
代表値とは?
代表値とは、データの特徴を1つの数値で表す統計量のことです。主なものとして以下の3つが挙げられます。
- 平均(相加平均):データ全体の合計をデータ数で割った値
- 中央値:データを並べたときに中央にくる値
- 最頻値:データの中で最も頻繁に出現する値
それぞれの特徴や活用場面を詳しく見ていきましょう。
平均(相加平均)とは?
計算方法
平均 = データの合計 ÷ データの個数平均
例えば、5人のテストの点数が [60, 70, 80, 90, 100] だった場合、 (60+70+80+90+100)÷ 5 = 80となり、平均は80点です。
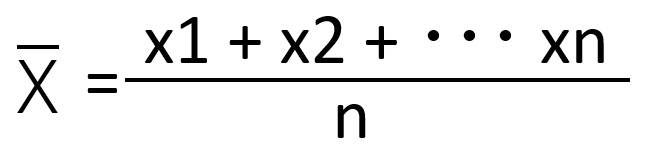
特徴
- すべてのデータを考慮するため、データの全体的な傾向を把握しやすい。
- 外れ値(極端に大きい or 小さい値)の影響を受けやすい。
活用シーン
- 企業の売上分析:平均売上を算出し、成長トレンドを分析。
- 学校の成績評価:生徒の成績の全体的な傾向を把握。
- 経済指標:国民の平均所得や平均寿命の算出。
中央値(メディアン)とは?
計算方法
データを 昇順または降順 に並べ、中央にくる値が中央値です。
例: [60, 70, 80, 90, 100] → 80(中央)
データの個数が偶数の場合は、中央2つの値の平均をとります。
例: [60, 70, 80, 90] → (70 + 80) ÷ 2 = 75
特徴
- 外れ値の影響を 受けにくい。
- 順位データ(順序尺度) に適している。
活用シーン
- 所得分析:平均所得よりも中央値のほうが、一般的な所得水準を示す。
- 不動産価格:極端に高い物件が平均を押し上げるため、中央値のほうが実態に近い。
- スポーツ記録:選手のパフォーマンス評価(特に外れ値を除きたい場合)。
最頻値(モード)とは?
計算方法
データの中で 最も多く出現する値 が最頻値です。
例: [10, 20, 20, 30, 30, 30, 40] → 最頻値は 30
特徴
- カテゴリデータ(名義尺度)にも適用できる。
- データの分布を直感的に理解しやすい。
- 複数の最頻値(多峰性分布) を持つことがある。
活用シーン
- アンケート調査:最も選ばれた回答を分析。
- マーケティング:最も売れている商品の価格帯を把握。
- 医学・薬学:特定の症状や副作用の頻度分析。
代表値の選び方
| 代表値 | 特徴 | 向いているデータ | 注意点 |
|---|---|---|---|
| 平均 | 全体の傾向を把握 | 正規分布に近いデータ | 外れ値の影響を受ける |
| 中央値 | 外れ値の影響を受けにくい | 偏った分布のデータ | データの個数が少ないと精度が低下 |
| 最頻値 | 直感的にわかりやすい | カテゴリデータ | 最頻値が複数ある場合がある |
まとめ
代表値の選び方がデータ分析の精度を左右します。
- 平均:全体的な傾向を知りたいとき。
- 中央値:外れ値があるデータを扱うとき。
- 最頻値:カテゴリデータを分析するとき。
適切な代表値を使い分け、より正確なデータ分析を行いましょう!



コメント