DS022:指数関数とlog関数の関係を理解し、片対数グラフ、両対数グラフ、対数化されていないグラフを適切に使いわけることができる
この記事で解決できる疑問
・「指数関数のグラフって急に大きくなって、傾向が見えない…」
・「片対数グラフや両対数グラフって、いつ使えばいいの?」
・「log関数との関係性がイマイチつかめない」
この記事では、こうした疑問に対して、対数・log関数の基本から、片対数・両対数グラフの使い分け方まで、丁寧に解説します。
数学やデータ分析を学ぶ初学者だけでなく、業務でグラフ作成をする方にとっても役立つ内容です。
指数関数とlog関数の関係
指数関数は、数値が急激に増える動きを示す関数です。
Y = 10^x
対数関数は、この指数関数の逆の関数です。
X = log10(Y)
この関係を理解しておくと、「指数的に増えるデータ」を「直線」で表現できるようになります。これが対数グラフの強みです。
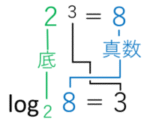
対数の種類
| 名称 | 説明 | 記号例 |
|---|---|---|
| 常用対数 | 底が10の対数 | log₁₀(x) |
| 自然対数 | 底がネイピア数e(約2.718) | ln(x) |
| 2進対数 | 底が2の対数(情報理論でよく使う) | log₂(x) |
片対数グラフとは?
片対数グラフは、縦軸または横軸のどちらか一方だけを対数スケールにしたグラフです。
例:Y = 10^X のグラフ
・通常グラフ → 急激に右上へ伸びてしまい、傾向が見えない
・片対数グラフ(縦軸log) → 直線に見える
つまり、指数関数の傾向を視覚的に把握したいときに有効です。
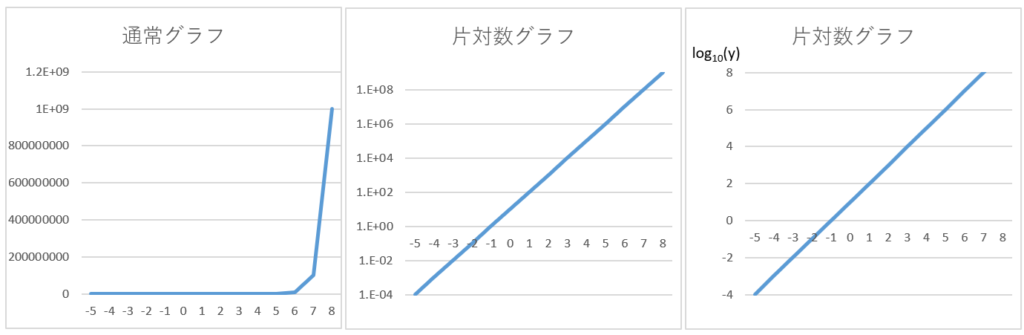
グラフから分かるように値が指数関数的に増加する。
通常グラフ (左) 傾向がほぼ表示できません。
片対数グラフ(中) 全体の傾向を確認する事が出来ます。
片対数グラフ(右) Ý軸の単位をlogに変更する事でメモリ表記をすっきりさせれる。
このグラフで使用した関数を底が10のlogに置き換えると下記のようになります。
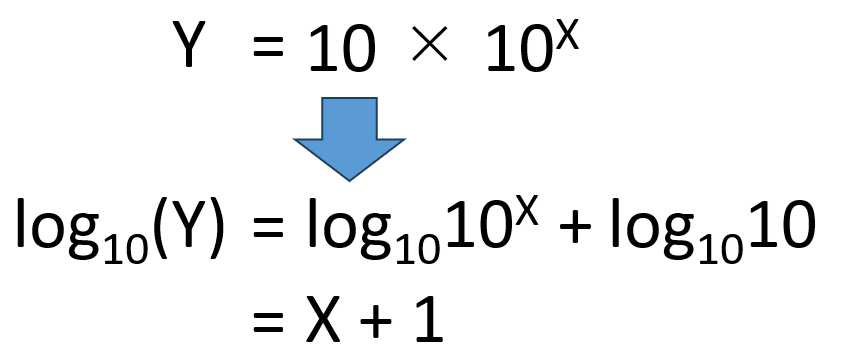
両対数グラフとは?
両対数グラフは、縦軸も横軸も対数スケールにしたグラフです。
例:Y = X² のグラフ
・通常グラフ → 下側がつぶれて見づらい
・両対数グラフ → 直線になる
両対数グラフは、べき乗関係(Y ∝ X^a)のデータを直線で表したいときに使われます。
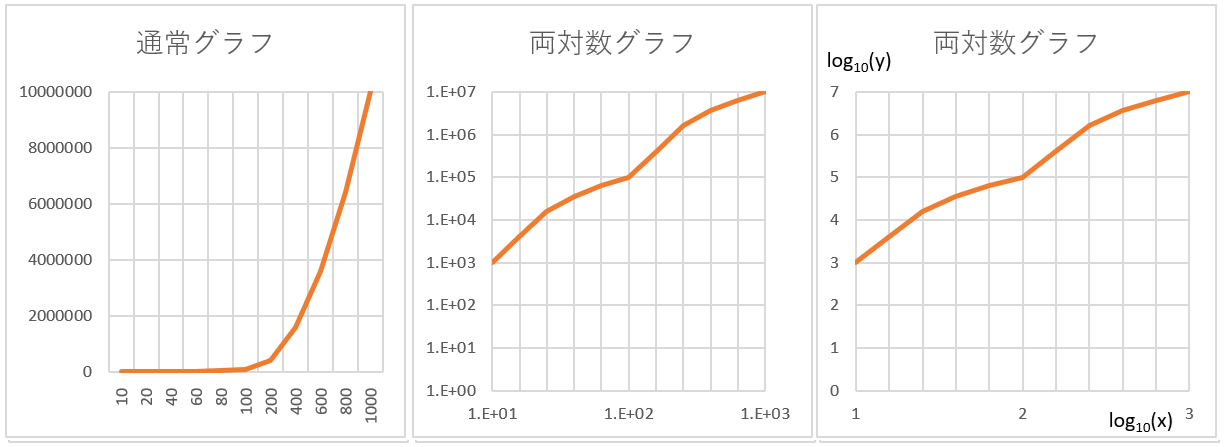
片対数グラフと同様に全体の傾向が読み取れるようになりました。このグラフで使用した関数を底が10のlogに置き換えると下記のようになります。
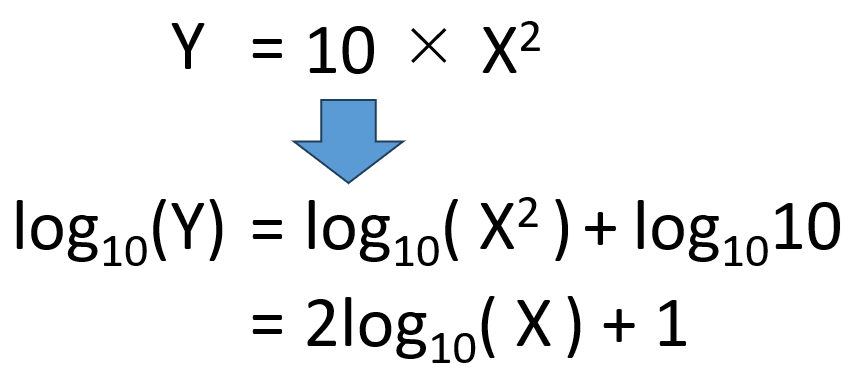
対数グラフの使いどころ
片対数グラフ : 指数的な増加・減少
両対数グラフ : べき乗の関係(例:Y=X^2)
・売上が時間とともに10倍、100倍と成長 → 片対数グラフ
・人口密度と都市の面積の関係 → 両対数グラフ
まとめ
・対数関数は、指数関数の逆関数
データが急激に増えるときは対数スケールで見ないと傾向がつかみにくい
・片対数グラフは指数関数的な変化を直線に見せる
・両対数グラフはべき乗関係の変化を直線に見せる
グラフはデータの傾向を正しく伝える道具です。見せ方を工夫するだけで、データの意味が伝わりやすくなります。



コメント