DS002:行列同士、および行列とベクトルの計算方法を正しく理解し、複数の線形式を行列の積で表現できる
この記事で解決できること
- ベクトルの基本的な概念が理解できる
- ベクトルの演算(加算・減算・内積・外積)ができるようになる
- 行列の基礎(正方行列、ゼロ行列、単位行列)を理解できる
- 応用問題に取り組む際の考え方が身につく
ベクトルは数学や物理の問題で頻繁に登場しますが、計算方法に苦手意識を持つ人も多いのではないでしょうか。本記事では、ベクトルの基礎から計算方法、応用例までをわかりやすく解説します。
ベクトルとは?
スカラーとベクトルの違い
- スカラー:数値のみで表される量(例:温度、質量)。
- ベクトル:大きさと向きを持つ量(例:速度、力)。
例
- 温度 30℃(スカラー)
- 北東方向に10m/sの風(ベクトル)
ベクトルは、数学では $(x, y)$ や $(x, y, z)$ という形式で表されます。
行列とは?
行列は、数値を並べた表のようなもので、数学やコンピュータサイエンスで広く用いられます。
正方行列
行と列の数が等しい行列を 正方行列 と呼びます。
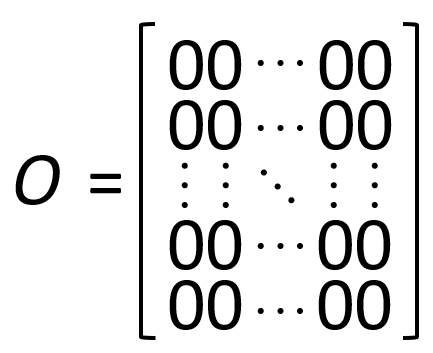
ゼロ行列
すべての要素が 0 である行列を ゼロ行列 と呼びます。
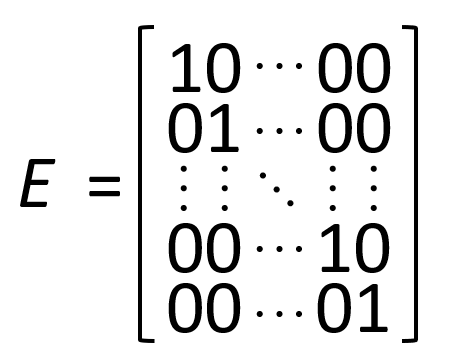
単位行列
対角成分が 1 で、それ以外が 0 の正方行列を 単位行列 と呼びます。単位行列は行列の積において 掛けても変化しない要素 となります。
ベクトルの基本演算
1. ベクトルの加算・減算
2つのベクトル {a} = (a_1, a_2) と {b} = (b_1, b_2) の加算・減算は、対応する成分ごとに計算します。
公式
{a}+{b}= ( a1 + b1 , a2 + b2 )
{a}- {b}= ( a1 − b1 , a2 − b2 )
例題
{a} = ( 3 , 4 ) , {b} = ( 1 , -2 ) のとき、
{a} + {b} = ( 4 , 2 )
{a} − {b} = ( 2 , 6 )
2. スカラー倍
ベクトル {a} = ( a_1 , a_2 ) を k 倍すると、
k{a}=( ka1 , ka2 )
例
k=2 {a} = ( 3 , 4 )
k{a} = ( 6 , 8 )
内積(ドット積)
ベクトルの 内積 は以下の公式で求めます。
a⋅b = a1b1 + a2b2
例 {a} = ( 3 , 4 ) , {b} = ( 1 , -2 )
3 × 1 + 4 × (−2) = 3 − 8 = (−5)
用途
- 2つのベクトルが直交しているかの判定(内積が0なら直交)
- 物理における仕事の計算
- 機械学習での類似度計算(コサイン類似度)
外積(クロス積)
2次元の場合、外積は以下の公式で計算します。
a × b = a1b2 – a2b1
例 {a} = ( 3 , 4 ) , {b} = ( 1 , -2 )
3 × (−2) + 4 × 1 = ー 6 − 4 = (−10)
用途
- 2つのベクトルが作る面積の計算
- 3Dグラフィックスや物理計算
- 力のモーメント計算
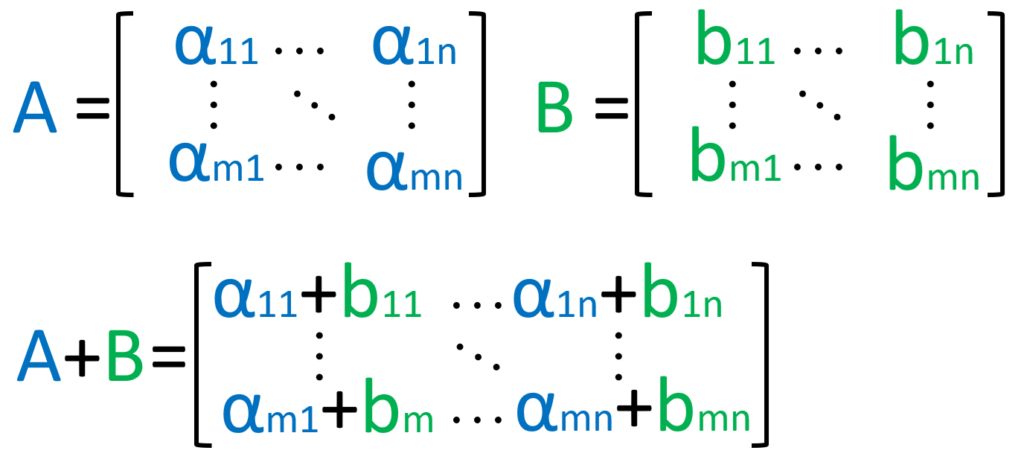
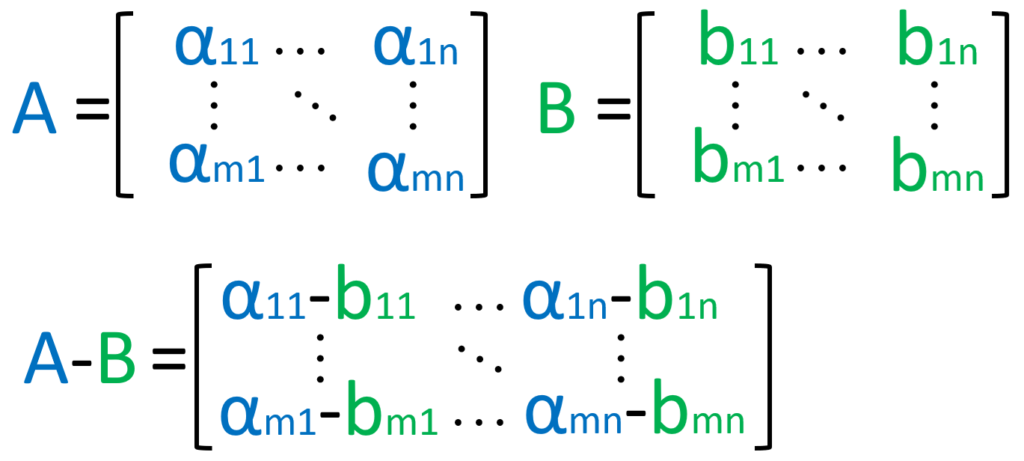
行列の加算・減算
行列の加算・減算は、同じサイズの行列同士でのみ行えます。
各成分ごとに加算・減算を行います。
加算の公式
減算の公式
行列のスカラー倍
行列をスカラー(数値)k 倍する場合、すべての成分に k を掛けるだけです。
公式
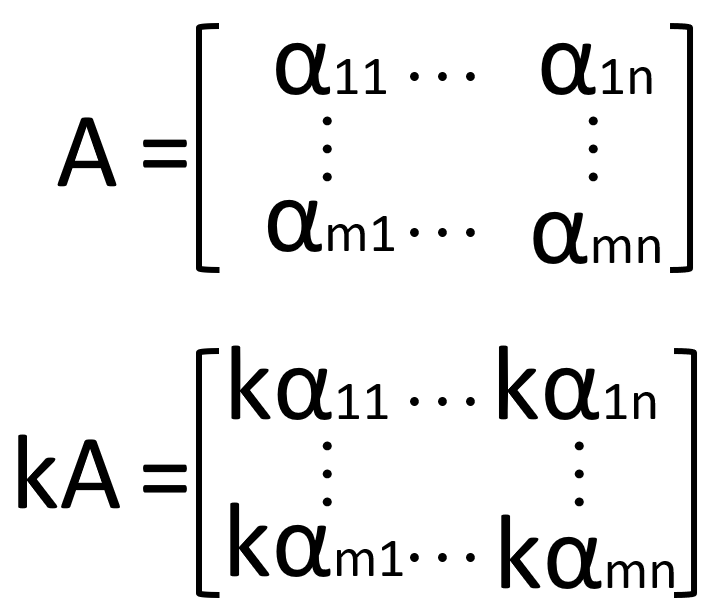
例題
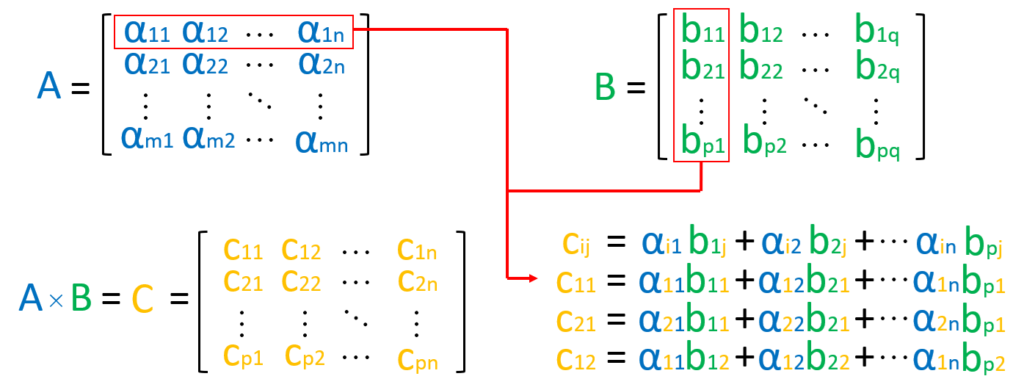
行列の積(行列 × 行列)
行列の積は、通常の数値の積とは異なり、行列のサイズに注意が必要です。
- {A }( m列 , n行 ) と {B }( n列 , p行 ) を掛ける場合、結果は m列 , p行 の行列 になる。
公式
例題
ベクトル計算の応用例
1. 物理(力の合成)
2つの力 {F_1} = ( 5 , 2 ) と {F_2} = ( -3 , 4 ) が働いているとき、合力は
( 5 + (−3) , 2 + 4 ) = ( 2 , 6 )
2. コンピュータグラフィックス
3Dモデルの描画では、ベクトルを使って光の当たり方や視点変換を計算します。
3. 統計学とデータ分析
主成分分析(PCA)などで、データの次元圧縮にベクトルが利用されます。
まとめ
ベクトルの計算は、数学だけでなく物理やデータ分析、3D技術など幅広く活用されます。
この記事のポイント
- ベクトルの基本概念(スカラーとの違い)
- 行列の基礎(正方行列、ゼロ行列、単位行列)
- ベクトルの加減算、スカラー倍、内積、外積
- 応用例(力の合成、3Dグラフィックス、統計)
ベクトルと行列を理解し、実践的に使えるようにしていきましょう!

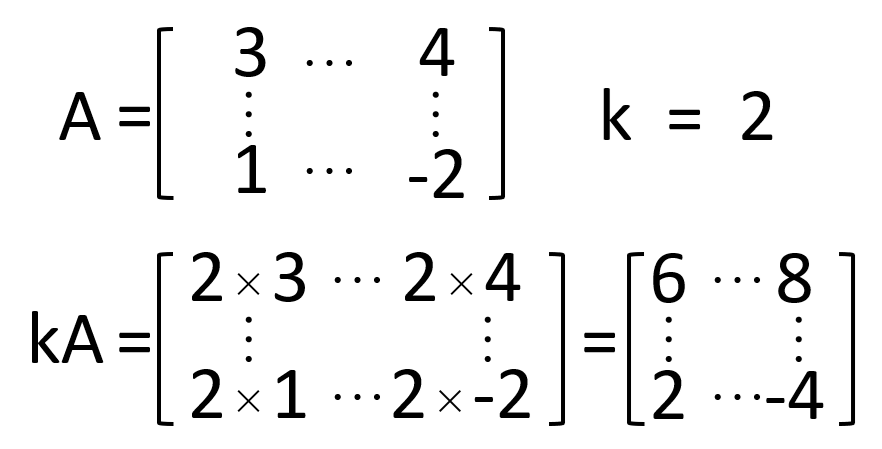



コメント