DS18:ピアソンの相関係数の分母と分子を説明できる
データサイエンティスト検定のスキルチェックリストDS18及びDS19に関する解説を行います。
ピアソンの相関係数:ピアソンの積率相関といい、2つの連続変数がどれだけ線形的に関連しているかを示す数値です。具体的には、その強さと方向(正の相関か負の相関か)を定量化します。この相関係数rは、-1から1の範囲で表され、r>0であれば正の相関、r<0であれば負の相関、r=0であれば無相関を示します。

共分散:共分散は、2つの変数の偏差積の平均です。具体的には、次のように表されます。
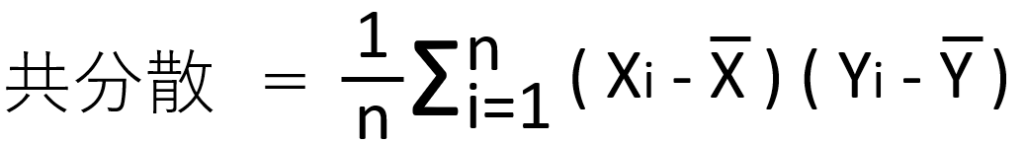
DS19:5つ以上の代表的な確率分布を説明できる
離散型確率分布
離散型確率分布:離散的な値をとる確率変数の確率分布のことです。これは、確率変数が一連の特定の値の中からひとつを取る場合に用いられます。さいころの目などが例としてあげられます。
ベルヌーイ分布:コイン投げや二者択一の試行結果モデリングで使用され、1回の試行で成功/失敗を取る離散型確率分布です。下記の式で確立分布が表されます。コイン投げにおけるコイントスなどはベルヌーイ試行と呼ばれます。
成功確率 p=P(X=1)
失敗確率 1-p=P(X=0)
二項分布:二項分布はベルヌーイ試行を複数回行った時の確立を考えたものです。例えば、コイン投げをX回行ったときに表がk回出る確率など。下記の式で表せます。
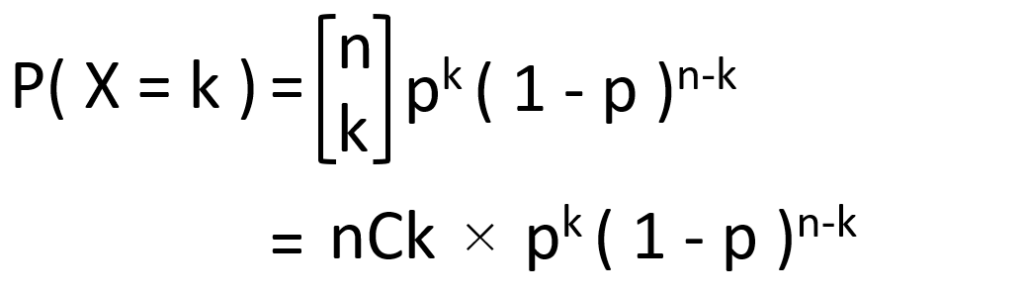
10回コイン投げを行い、表が出る確率は次のように表します。
X ~ Binomial(n=10,p=0.5) ・・・Xが二項分布に従うという前提を記載。
P(X=10) = 1/1024 ・・・結果、確立は1/1024であることを示す。
ポアソン分布:ポアソン分布では、単位時間や単位面積あたりに平均 λ 回発生する事象の確率分布を考えます。時間あたりの電話の着信数や、ある地域で交通事故が発生しない確率などがあります。
確率変数Xがポアソン分布に従うとき、X∼Poisson(λ)と表され、次の式で確立を求めます。
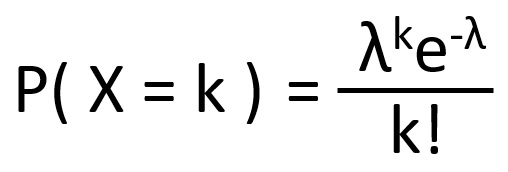
「λ」:平均の事象発生回数(非負の実数)、「e」:自然対数の底(ネイピア数)、「k」:成功回数
連続型確率分布
連続型確率分布:連続的な値を取る確率変数に対する確率分布です。これらの分布は、離散型確率分布とは異なり、確率変数が連続的な値の範囲である場合に適用されます。
正規分布:平均値、中央値、最頻値が一致した理論的に扱いやすい分布です。正規分布はその特性により多くの統計的手法の基礎となっています。分布の形状はベル型曲線として知られ、その形状は平均と分散によって決まります。
指数分布:到着間隔のモデルや故障の時間間隔、サービス時間のモデル化などに広く使用され、電話の着信間隔や交通信号の待ち時間などが指数分布で記述されることがあります。
カイ二乗分布:ふたつの標準正規分布に従う確率変数を二乗して足し合わせたものが従う分布です。仮説検定や分散分析、因子分析などで重要な役割を果たします。



コメント