DS020:二項分布は試行回数が増えていくとどのような分布に近似されるかを知っている
本記事で解決できる課題
- 二項分布が試行回数によってどのように変化するのか知りたい
- 正規分布と二項分布の関係を理解したい
- 実際のデータ分析でどのように活用できるのか知りたい
データ分析や統計学において、確率分布を理解することは重要です。特に、二項分布は「成功・失敗」のように2つの結果を持つ試行に適用され、試行回数が増えると正規分布に近づく性質があります。本記事では、この関係を分かりやすく解説します。
二項分布とは?
二項分布は、以下の条件を満たす確率分布です。
- 各試行は「成功」または「失敗」の2つの結果しかない
- 各試行の成功確率は一定
- 試行は独立している
例えば、コイン投げで「表」が出る確率を考えます。
- コインを1回投げる → 表が出る確率 = 50%
- 10回投げて表が出る回数は? → これが二項分布に従う
二項分布の確率質量関数(PMF)は次の式で表されます。
- n:試行回数
- k:成功回数
- p:成功確率
例えば、コイン投げ(p=0.5)で10回投げたとき、5回表が出る確率はこの式を用いて求められます。
試行回数が増えるとどうなる?
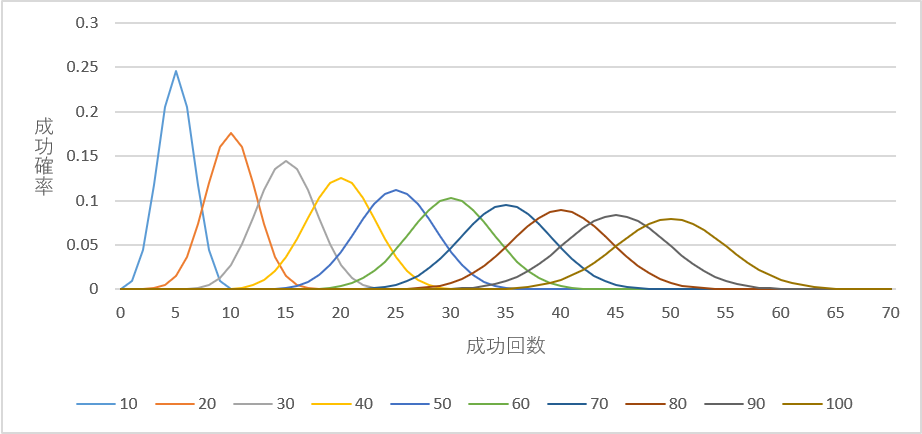
試行回数(nn)が増えると、二項分布は次のように変化します。
- 最初はばらつきが大きい
- 例:コインを5回投げると、表が出る回数は 0 ~ 5 まで幅広く分布する。
- 試行回数が増えると中央に集まる
- 例:コインを100回投げると、表が出る回数は45~55回の範囲に集中する。
- 試行回数が十分に大きくなると、正規分布に近づく
- 例:コインを1000回投げると、表が出る回数はおよそ500回を中心とする正規分布に近い形になる。
この現象は「中心極限定理」によって説明されます。
中心極限定理とは?
中心極限定理とは、多くの試行の結果を足し合わせると、その分布が正規分布に近づくという定理です。
具体例
- サイコロを1回振ると1~6の目が出る確率は均等。
- 100回振って出た目の平均を取ると、理論的には「3.5」に近づく。
- これを何度も繰り返すと、平均値の分布は正規分布に近くなる。
二項分布でも、試行回数が増えると成功回数の分布が正規分布に近づきます。
実際のデータ分析への応用
A/Bテスト
A/Bテストでは、Webサイトの2つのデザイン(AとB)のどちらがユーザーのクリック率を高めるかを調査します。
- Aのクリック率:5%
- Bのクリック率:7%
- 1000人に表示してクリック回数を記録
このとき、クリックの有無は二項分布に従います。試行回数が増えれば正規分布とみなして統計検定を適用できます。
品質管理
工場の製品検査で「不良品である確率」を管理する際、
- 不良率5%
- 100個検査したときの不良品数
これは二項分布に従いますが、多くのデータを取ると正規分布に近づき、管理基準を設定しやすくなります。
まとめ
- 二項分布は「成功/失敗」の確率をモデル化する分布
- 試行回数が増えると分布が中央に集中し、正規分布に近づく
- 中心極限定理により、多くのデータを取れば正規分布として扱える
- A/Bテストや品質管理など、多くの分野で応用される
確率分布を理解すると、データ分析の幅が広がります。ぜひ、実際のデータに適用してみてください!

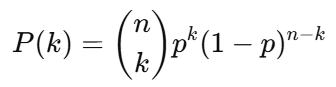

コメント