DS3:逆行列の定義、および逆行列を求めることにより行列表記された連立方程式が解けることを理解している
この記事で解決できること
行列の逆行列(逆数のようなもの)について学びたい方へ向けて、以下の内容を解説します。
- 逆行列とは何かを理解できる
- 逆行列を求める方法が分かる
- 逆行列を使って連立方程式を解く方法を学べる
- 逆行列の実用的な活用例を知ることができる
「行列って何?」という方でも分かるように、できるだけ噛み砕いて説明していきます!
逆行列とは?
逆行列とは、ある行列 に対して、「掛けると単位行列 I になる行列」 のことです。
単位行列とは、普通の数でいうところの「1」のような存在で、例えば2×2行列の単位行列は次のようになります。
ある行列 に対して、その逆行列を A^{-1}とすると、以下の関係が成り立ちます。
逆行列の求め方(2×2行列の場合)
二次正方行列の逆行列の求め方を説明します。二次正方行列の場合は下記の式で求める事が出来ます。
この公式はad-bc≠0の時に成り立ち、ad-bcはAの行列式と呼び、「det(A)」もしくは「|A|」で表します。
≪公式≫
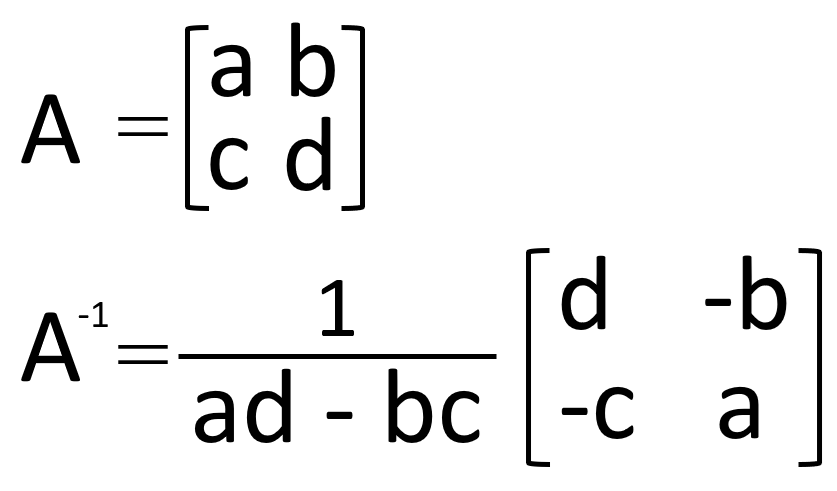
≪例≫
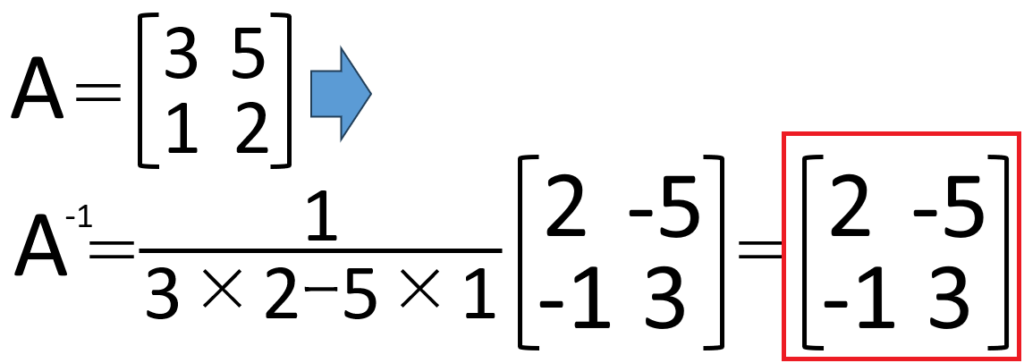
逆行列が存在しない場合
この公式はad-bc≠0の時、逆行列は存在しません。例えば、
となり、この場合、逆行列は求められません。
逆行列を使った連立方程式の解き方
逆行列は連立方程式の解を求めるのにも使えます。
例えば、次の連立方程式を行列で表します。

次に両辺に逆行列を乗算する事で解を得られます。
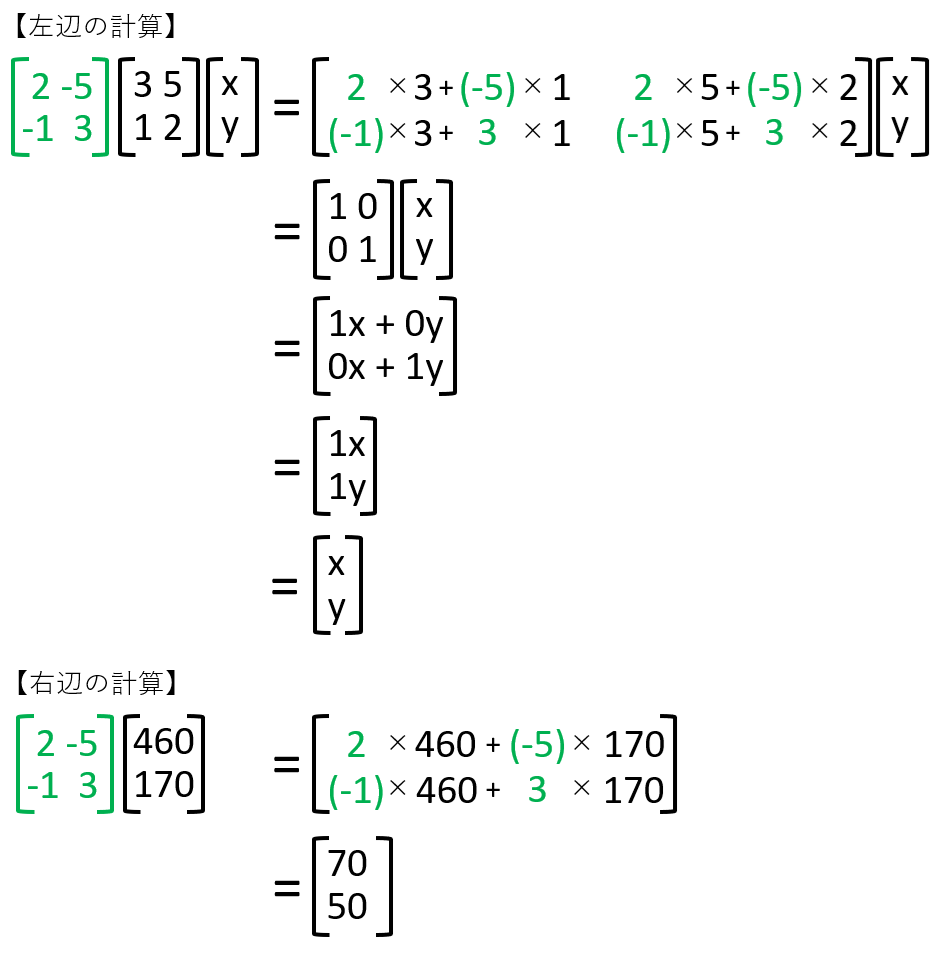
多次元での逆行列の求め方
前3×3以上の行列の場合、掃き出し法(ガウス・ジョルダン法)や余因子行列を用いた方法などを使って求めることができます。下記に掃き出し法について記載します。
逆行列を求めたい行列Aの右隣に単位行列を付加する。
「行基本変形」という操作を繰り返し行い「単位行列」「逆行列」の形にする。
左側の単位行列お取り除いた残りが行列Aの逆行列である。
行基本変形では下記の3つの操作を行うことが出来る。
① 要素の交換:行列の行を交換する。
② 定数倍 :行の全要素を定数倍する。
③ 行の加算 :行に別の行の定数倍を加える。
手順例
1.逆行列を求めたい行列Aの右隣に単位行列を付加する。
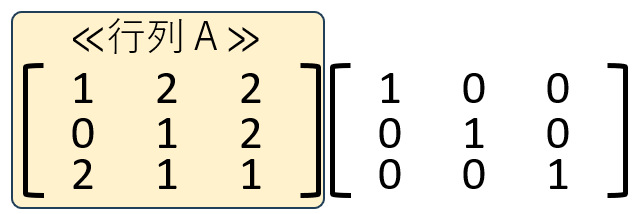
2.1行目を-2倍した値を3行目に加算する。
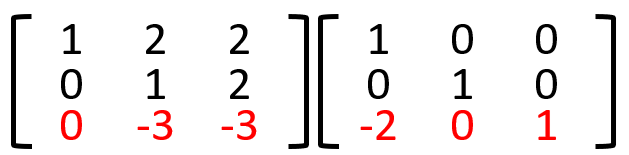
3.2行目を-2倍した値を1行目へ加算する。
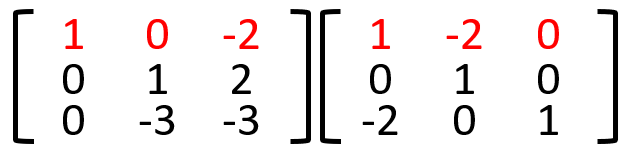
4.3行目を-1/3倍する。
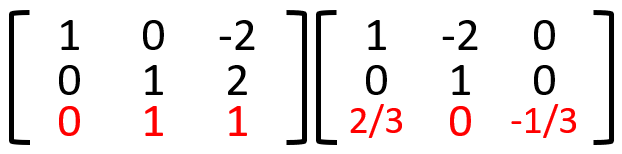
5.2行目を-1倍した値を3行目へ加算する。
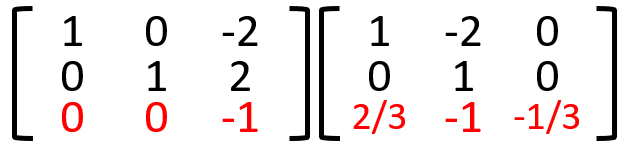
6.3行目を-2倍した値を1行目へ加算する。
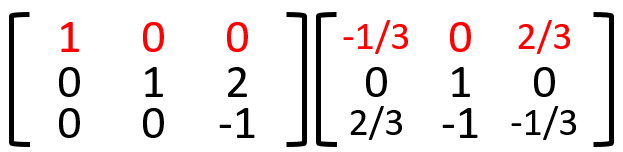
7.3行目を2倍した値を2行目へ加算する。
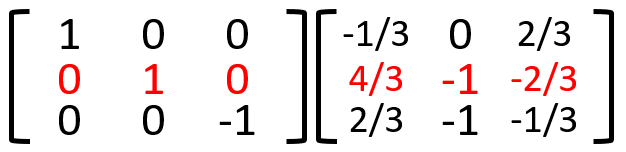
8.3行目をー1倍する事で左の行列が単位行列となり、右側に逆行列が完成する。
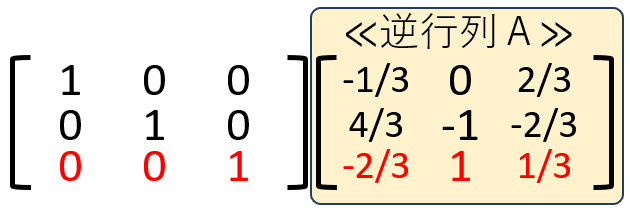
逆行列の活用例
① 画像処理(フィルタ変換)
デジタル画像の加工には行列演算が使われており、逆行列を用いて特定のフィルター処理を行うことがあります。
② 物理学(力の解析)
逆行列は、剛体の力学計算や電気回路の解析など、様々な場面で利用されます。
③ 統計学(回帰分析)
最小二乗法を使った回帰分析では、逆行列を用いて係数を求めることがあります。
まとめ
逆行列は「掛けると単位行列になる行列」
2×2ぎょうれつなら公式で簡単に求められる。
連立方程式の解法にも応用できる。
画像処理や統計分析などで幅広く活用できる。

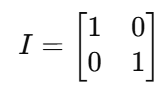
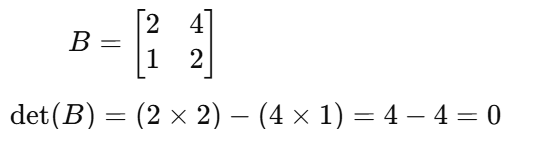


コメント