DS054:ある変数が他の変数に与える影響(因果効果)を推定したい場合、その双方に影響を与える共変量(交絡因子)の考慮が重要であると理解している(喫煙の有無と疾病発症の双方に年齢が影響している場合など)
データ分析における変数と因子の関係
データ分析を行う際、変数同士の関係性を理解することは重要です。本記事では、独立変数、従属変数、要因、交絡因子、中間因子の違いとその関係性を解説します。
変数の基本概念
独立変数(Independent Variable)
独立変数とは、他の変数に影響を与える要因となる変数です。例えば、価格が売上に与える影響を調べる場合、価格が独立変数となります。
従属変数(Dependent Variable)
従属変数とは、独立変数の変化によって変動する変数です。先ほどの例では、売上が従属変数になります。
| 独立変数 | 従属変数 |
|---|---|
| 広告費 | 商品の売上 |
| 勉強時間 | 試験の成績 |
| 気温 | アイスクリームの売上 |
データ分析における要因とその影響
要因(Factor)
要因とは、従属変数に影響を及ぼす変数です。多くの場合、要因は独立変数と考えられますが、複数の要因が組み合わさることもあります。
例えば、商品の売上には「価格」「広告費」「店舗の立地」など複数の要因が影響を与えます。
交絡因子(Confounding Variable)
交絡因子とは、独立変数と従属変数の間に影響を与え、本来の因果関係を歪める可能性がある変数です。
| 独立変数 | 従属変数 | 交絡因子 |
|---|---|---|
| 運動量 | 体重の減少 | 食事の摂取量 |
| 勉強時間 | 試験の成績 | 事前の学力 |
| コーヒー摂取量 | 心臓病の発生率 | 喫煙習慣 |
交絡因子を適切に考慮しないと、誤った結論を導く可能性があります。
中間因子(Mediating Variable)
中間因子とは、独立変数と従属変数の間に位置し、影響を媒介する変数です。
| 独立変数 | 中間因子 | 従属変数 |
|---|---|---|
| 広告費 | ブランド認知度 | 商品の売上 |
| 運動時間 | 基礎代謝の向上 | 体重の減少 |
| 教育レベル | 収入 | 生活満足度 |
中間因子の影響を分析することで、より詳細な因果関係を明らかにすることができます。
変数と因子の関係を考慮したデータ分析
データを分析する際には、以下の点を意識するとより正確な分析が可能になります。
- 独立変数と従属変数の関係を明確にする
- 交絡因子を排除するための統計手法(多変量解析、回帰分析など)を活用する
- 中間因子の影響を考慮したモデルを構築する
適切な変数の設定と因果関係の理解によって、データの正確な解釈が可能となります。
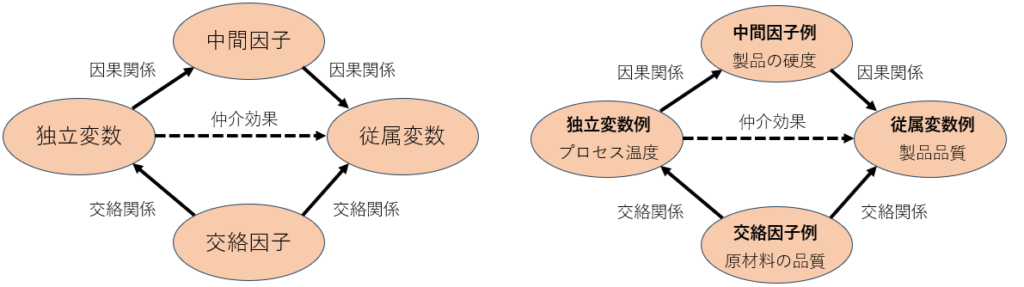
変数と因子の関係例
以下に、独立変数・従属変数・要因・交絡因子・中間因子が登場する関係例を示します。
例1: 広告費と売上の関係
- 独立変数: 広告費
- 従属変数: 商品の売上
- 交絡因子: 季節や市場の需要変動
- 中間因子: ブランド認知度
- 要因: 販売戦略、競合の影響
例2: 運動と体重減少の関係
- 独立変数: 運動時間
- 従属変数: 体重の減少
- 交絡因子: 食事の摂取量、遺伝的要素
- 中間因子: 基礎代謝の向上
- 要因: 健康状態、ライフスタイル
例3: 教育と収入の関係
- 独立変数: 教育レベル
- 従属変数: 収入
- 交絡因子: 家庭環境、社会経済的地位
- 中間因子: 職業スキルの向上
- 要因: 業界の市場価値、経験年数
まとめ
| 用語 | 定義 | 例 |
|---|---|---|
| 独立変数 | 他の変数に影響を与える変数 | 価格、勉強時間 |
| 従属変数 | 独立変数の影響を受ける変数 | 売上、試験の成績 |
| 要因 | 従属変数に影響を与える要素 | 広告費、店舗の立地 |
| 交絡因子 | 独立変数と従属変数の関係を歪める変数 | 食事の摂取量、喫煙習慣 |
| 中間因子 | 独立変数と従属変数の間で媒介する変数 | ブランド認知度、基礎代謝 |
データ分析では、単純な相関関係だけでなく、因果関係を適切に把握することが求められます。これらの概念を活用し、より正確な分析を行いましょう。



コメント