RMSE、MAE、MAPE、決定係数：評価指標の違いと選び方

DS155：RMSE（Root Mean Square Error）、MAE（Mean Absolute Error）、MAPE（Mean Absolute Percentage Error）、決定係数といった評価尺度を理解し、精度を評価できる

DS155：RMSE（Root Mean Square Error）、MAE（Mean Absolute Error）、MAPE（Mean Absolute Percentage Error）、決定係数といった評価尺度を理解し、精度を評価できる

機械学習や統計分析において、モデルの精度を評価することは重要です。本記事では、代表的な評価指標であるRMSE（Root Mean Square Error）、MAE（Mean Absolute Error）、MAPE（Mean Absolute Percentage Error）、決定係数（R²）について解説します。

この記事で解決できる課題

誤差をどのように評価すればよいかわからない
RMSEやMAEの違いが理解できない
どの指標を選べばよいのか迷っている

これらの疑問に対して、それぞれの指標の特徴や適用場面を解説し、適切な評価指標の選び方を説明します。

RMSE（Root Mean Square Error）

RMSE（平方平均二乗誤差）は、予測値と実際の値の誤差の二乗平均の平方根を取ったものです。

特徴

大きな誤差に敏感：誤差を二乗するため、極端な外れ値（異常値）があるとRMSEが大きくなります。
単位が元のデータと同じ：直感的に解釈しやすいですが、外れ値に影響されやすい点に注意が必要です。

使用場面

外れ値を特に重視したい場合
予測誤差の平均を直感的に把握したい場合

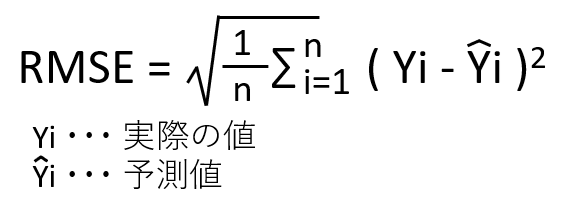
MAE（Mean Absolute Error）

MAE（平均絶対誤差）は、予測値と実測値の誤差の絶対値の平均を求めたものです。

特徴

外れ値に比較的影響を受けにくい：RMSEと異なり二乗を取らないため、大きな誤差が過度に影響を与えません。
単位が元のデータと同じ：RMSEと同様、解釈しやすい指標です。

使用場面

外れ値の影響を抑えつつ、全体の誤差を評価したい場合
予測の誤差を単純に測定したい場合

MAPE（Mean Absolute Percentage Error）

MAPE（平均絶対パーセンテージ誤差）は、誤差を実測値に対する割合で示し、それを平均した指標です。

特徴

スケールに依存しない：パーセンテージで誤差を示すため、異なるデータセット間で比較しやすい。
実測値が0に近いと計算が不安定：0に近い値を持つデータでは、極端な誤差が発生する可能性があります。

使用場面

単位の異なるデータを比較したい場合
誤差を相対的に評価したい場合

決定係数（R²）

決定係数（R²）は、モデルがどの程度データの変動を説明できているかを示す指標です。

特徴

1に近いほど良いモデル：1に近いほど説明力が高く、0に近いとランダムな予測と変わらない。
負の値を取ることもある：モデルが平均値を用いた予測よりも精度が低い場合、負の値を取ることがあります。

使用場面

回帰モデルの適合度を測定したい場合
予測の説明力を評価したい場合

まとめ：どの指標を使うべきか？

指標	特徴	使用場面
RMSE	外れ値に敏感、単位は元のデータと同じ	外れ値を考慮したい場合
MAE	外れ値の影響が少なく解釈が簡単	誤差をシンプルに測定したい場合
MAPE	パーセンテージで表現、異なるデータ間で比較可能	スケールの異なるデータを扱う場合
決定係数（R²）	モデルの説明力を評価	回帰モデルの適合度を知りたい場合