SD015:標準正規分布の平均と分散の値を知っている
「正規分布ってよく聞くけど、実際どんな特徴があるの?」
「標準正規分布って何が特別なの?」
「正規分布表を使って確率を求めたいけど、どう計算するの?」
この記事では、そんな疑問を持つ方に向けて、標準正規分布の平均・分散や、正規分布から標準正規分布への変換方法(標準化)をやさしく解説します。これを知れば、統計問題で確率を計算したり、品質管理で不良率を見積もるといった場面でも役立ちます。
正規分布とは?
正規分布は、データ分析や統計学の基礎としてよく登場する分布です。
「釣鐘型」や「ベルカーブ」とも呼ばれ、平均値を中心に左右対称な形をしています。
例えば、「身長」、「テストの点数」、「製品の寸法」など、自然界や社会で見られる多くのデータが近似的に正規分布に従います。正規分布には以下の特徴があります。
平均(μ)
分布の中心位置を示します。標準偏差(σ)
データがどれくらい広がっているか(ばらつき)を示します。
これらによって、正規分布の形状は決まります。
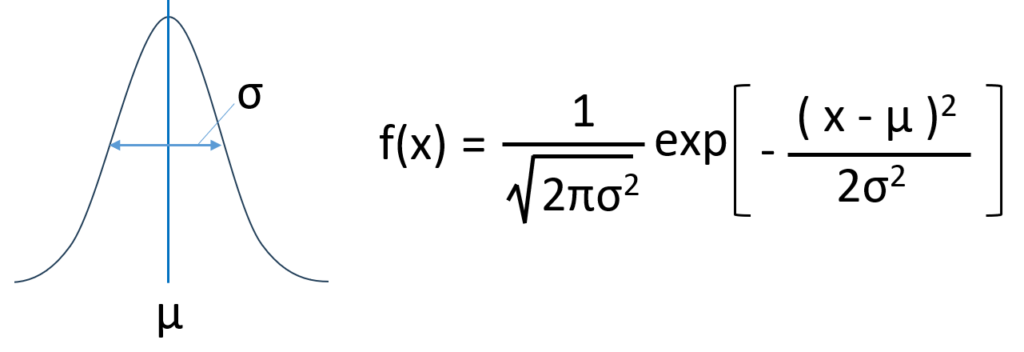
標準正規分布の平均と分散
数ある正規分布の中でも、特に重要なのが 標準正規分布 です。
・平均(μ)= 0
・分散(σ²)= 1(つまり標準偏差σ=1)
という特別な形の正規分布を指します。
この標準正規分布は、あらかじめ累積確率が表(Z表)としてまとめられており、
複雑な計算をせずに確率を調べることができます。
正規分布の標準化(Z変換)
しかし実際のデータは、平均や標準偏差が0や1ではない正規分布であることがほとんどです。
そこで使うのが 標準化(Z変換)。次の式で変換を行うことで、任意の正規分布から標準正規分布に変換できます。
Z = ( X - μ ) ÷ σ
これにより、「Xが平均からどれだけ離れているか」、「それが標準偏差の何倍か」を求めることができ、Z表を使って確率を簡単に調べられるようになります。
例題:Xが75以下となる確率
例題設定
平均μ=70、標準偏差σ=5の正規分布に従う変数Xについて、
Xが75以下になる確率を求めたいとします。
標準化(Z値)の計算
Z = ( 75 - 70 ) ÷ 5 = 1
つまり、X=75 は平均から1σ分上に離れた位置にあります。
Z表を使って確率を求める
標準正規分布表(Z表)で Z=1 の値を調べると、以下のようになります。
つまり、Xが75以下となる確率は 約84% です。
標準正規分布を使うメリット
正規分布は、どのような平均や標準偏差でも形状が決まっています。
しかし、個別に毎回積分で確率を求めるのは大変です。
そのため、「まずZ変換で標準正規分布に揃える」、「用意されたZ表を使って確率を調べる」という方法が取られます。これにより、どんな正規分布でも簡単に確率を求めることができるのです。
まとめ
・標準正規分布 は平均0、分散1の特別な正規分布。
・任意の正規分布はZ変換で標準正規分布に変換できる。
・標準正規分布表(Z表)を使うことで、確率を手軽に求められる。
これを知っておくと、品質管理や試験の合格率計算など、日常業務や学習でも大いに役立ちます。



コメント