DS007:積分と面積の関係を理解し、確率密度関数を定積分することで確率が得られることを説明できる
この記事で解決できる悩み
・「積分って結局、何を求めているの?」
・「確率密度関数と積分の関係がよく分からない…」
・「試験や実務で積分が出てくるけど、いまいちピンとこない」
そんな疑問を持つ方に向けて、本記事では「積分の意味」と「確率密度関数における使われ方」について、具体例を交えてわかりやすく解説します。
積分とは?グラフの“面積”を求めるもの
まず、積分には大きく分けて「不定積分」と「定積分」の2種類があります。
不定積分とは
不定積分とは、「ある関数の微分前の状態(原始関数)を求める操作」です。
例えば、関数 f(x) = 3x² を微分すると f'(x) = 6x になります。逆に、 6x から元の関数を求めるのが不定積分です。これは“面積”とは直接関係ないですが、後述する定積分を行うための準備として使われます。

定積分とは
定積分は、「ある関数のグラフとx軸で囲まれた“面積”を求める操作」です。
例えば、f(x) = 3x² のグラフにおいて、x=0〜1の区間の面積は次のように求めます。
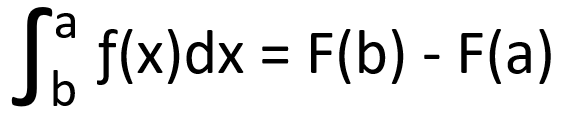
この「F(b) – F(a)」という数値が、関数とx軸で囲まれた部分の面積を表しています。
ポイント:積分の記号「∫」は、面積の総和(合計)を求める記号です。
確率密度関数とは?確率を面積で表す考え方
次に、積分が「確率」とどう関係するのかを見ていきます。
確率密度関数(PDF)とは
確率密度関数(Probability Density Function)は、「連続的な数値データに対する確率の分布を表す関数」です。例えば身長や体重のような連続データに使われます。離散的なデータ(例:サイコロの出目)の場合、ある値そのものに確率が定義されます。しかし連続データでは「ある値ぴったりに出る確率は0」となってしまいます。
そこで登場するのが定積分。ある範囲内に値が収まる確率を、確率密度関数を使って積分することで求めます。
積分で確率を求める
例えば、0〜1の範囲に値が収まる確率を求めたいとき、次のように定積分を使います。
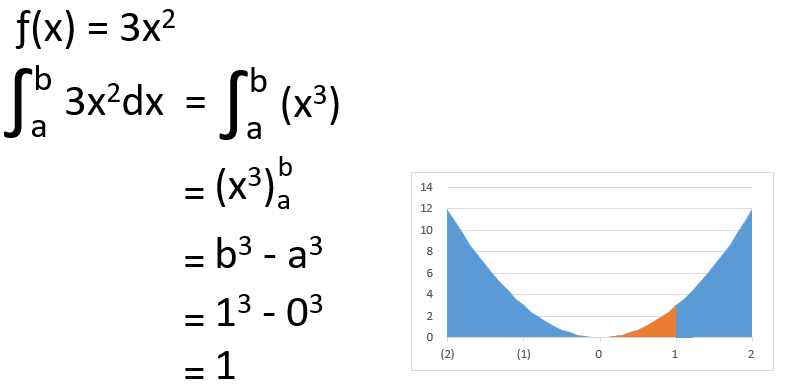
この積分結果が「0から1の間にデータが存在する確率」として表されます。
このように、確率=面積という考え方が、確率密度関数では重要になります。
まとめ:積分は“面積”と“確率”をつなぐ橋
この記事では以下のことを解説しました。
・積分には不定積分と定積分がある
・定積分は関数のグラフとx軸で囲まれた面積を求める
・確率密度関数では、範囲内にデータが存在する確率を定積分で計算する
積分=難しい数学、と構えてしまいがちですが、「面積」や「確率」という身近な概念とつながっていると分かれば、ずっと理解しやすくなります。ぜひ、試験対策やデータ分析の理解に役立ててみてください。



コメント