DS014:母(集団)平均と標本平均、不偏分散と標本分散がそれぞれ異なることを説明できる
この記事で解決できる疑問
・「母集団」と「標本」って何が違うの?
・母平均と標本平均って同じように見えるけど、どう違うの?
・「不偏分散」と「標本分散」の違いがよくわからない…
・統計で使われる用語が難しくて挫折しそう…
こうした悩みをお持ちの方に向けて、この記事では母集団と標本の違い、平均や分散の考え方の違いを、数式だけでなく図や具体例を交えながらわかりやすく説明します。
初学者の方にも理解できるように丁寧に解説していきます。
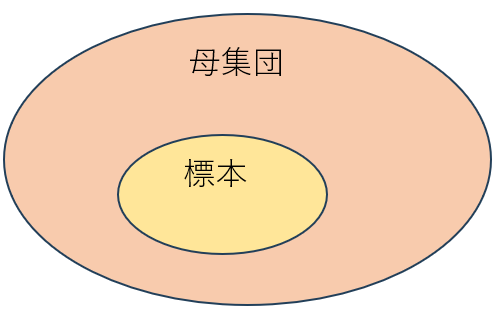
母集団と標本の違いとは?
母集団とは?
母集団とは、統計的な分析の対象となる全体の集まりを意味します。
例えば
・「日本の全成人」
・「ある商品の購入者全体」
・「すべての工場製品」
のように、対象となる“すべて”の集合が母集団です。
標本とは?
一方で、標本とは母集団から一部を取り出したサンプルのことです。母集団全体を調査するのはコストも時間もかかるため、現実的にはこの標本を調べて母集団の傾向を推測します。
例:全国の高校生の学力を調査したいが、全員を調べるのは困難なので、各地域の一部高校生(標本)を調査する。
母平均と標本平均の違い
母平均(μ:ミュー)
母平均とは、母集団に含まれるすべてのデータの平均値です。すべての情報を元にしているため、理想的な「真の平均」と言えます。しかし、実際には母集団の全データを取得できることは稀なので、次の標本平均が使われます。
標本平均(x̄:エックスバー)
標本平均は、標本から得られたデータの平均です。これは、母平均を推測する目的で使われる統計量です。
ただし、標本の取り方や数が不適切だと母平均からズレる可能性もあります。
母分散・標本分散・不偏分散とは?
母分散(σ²:シグマ二乗)
母分散は、母集団全体のデータのばらつきの度合いを表す指標です。母平均から各値がどれだけ離れているかを二乗して平均を取ります。
標本分散
標本分散は、標本データのばらつきを測る指標ですが、「n」で割って計算すると過小評価になる傾向があります。これは、標本が母集団を完全には代表できないためです。
不偏分散
不偏分散とは、標本分散のバイアス(過小評価)を補正した値です。「n」ではなく「n-1」で割ることで、母分散の推定値としてより適切になります。
不偏分散の式
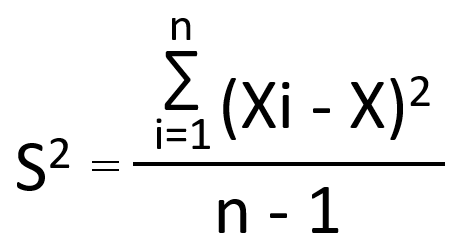
この補正は「自由度を1減らす」とも表現されます。
なぜ「n-1」で割る?不偏分散の考え方
これはよくある疑問です。
標本平均 (xˉ)を使って分散を計算する際、1つの自由度がすでに使われている(つまりデータの1個分の情報が制限されている)ため、残るのは「n-1個分の自由度」です。
例:テストの点数データ(5人分)から平均を出した後、その平均を使ってばらつきを調べるとき、すでに平均に情報を1つ使ってしまっているので、自由度は「5-1=4」となります5. 実生活にどう役立つ?平均・分散の使い道
例1:マーケティング
ある商品の売上データから、平均購入金額やそのばらつきを計算して、ターゲット層の絞り込みに活用できます。
例2:品質管理
工場で製品の長さや重さを測定して、不良品が一定の基準からどれだけ外れているかを分散でチェックします。
まとめ
母集団と標本、母平均と標本平均、不偏分散と標本分散は、統計学の基礎であり、現実の問題解決にも直結する知識です。
| 用語 | 内容 |
|---|---|
| 母集団 | 調査対象の全体 |
| 標本 | 母集団から抜き出した一部のデータ |
| 母平均 | 母集団すべての平均 |
| 標本平均 | 標本データの平均 |
| 母分散 | 母集団全体のばらつき |
| 標本分散 | 標本データのばらつき(nで割る) |
| 不偏分散 | 母分散の推定値(n-1で割る) |



コメント