DS001:ベクトルの内積に関する計算方法を理解し、線形式をベクトルの内積で表現できる
この記事で解決できること
・ベクトルって何?方向や大きさってどういう意味?
・内積の計算方法がわからない…
・線形形式って難しそうだけど、ベクトルで表せるの?
そんな疑問を持つ方に向けて、本記事ではベクトルの基礎から内積の意味、線形形式との関係まで、図や例を交えてやさしく解説します。数学が苦手な方や、統計・機械学習の前提知識として理解したい方にもおすすめです。
ベクトルとは?
ベクトルとは、複数の数値(成分)からなる「方向」と「大きさ」を持つ量です。数式の世界では、点や変化量などを表現するのによく使われます。
ベクトルの例
・二次元ベクトル:(3, 4)三次元ベクトル:
・(1, 0, -2)
このように、数値の組を矢印(向きと長さ)で表すとイメージしやすいです。
用語の整理
| 用語 | 意味 |
|---|---|
| 要素 | ベクトルに含まれる各数値 |
| スカラー | 単なる数値(例:3や-1.5) |
| 行ベクトル | 要素が横に並んでいる:(1, 2, 3) |
| 列ベクトル | 要素が縦に並んでいる: 1 2 3 |
| ゼロベクトル | すべての要素が0のベクトル:(0, 0, 0) |
| 単位ベクトル | 長さが1のベクトル(例:(1, 0)) |
ベクトルの計算方法
ベクトルの加算
同じ次元のベクトル同士で、対応する要素を足します。
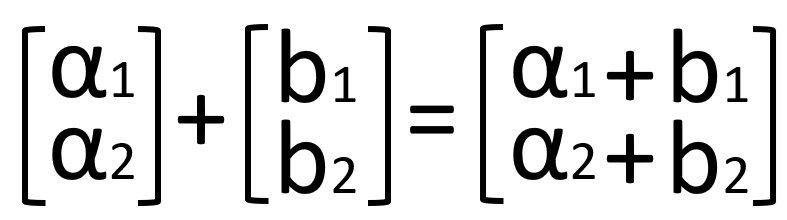
スカラー倍
ベクトルにスカラーをかけると、各要素にその値が乗算されます。
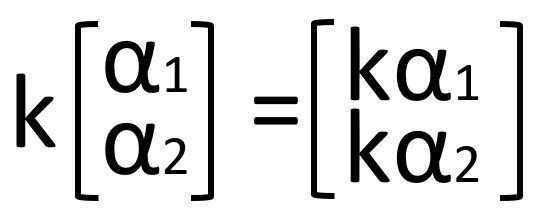
ベクトルの内積(ドット積)
内積とは、同じ次元の2つのベクトルの対応要素を掛け算し、その結果をすべて足し合わせたものです。
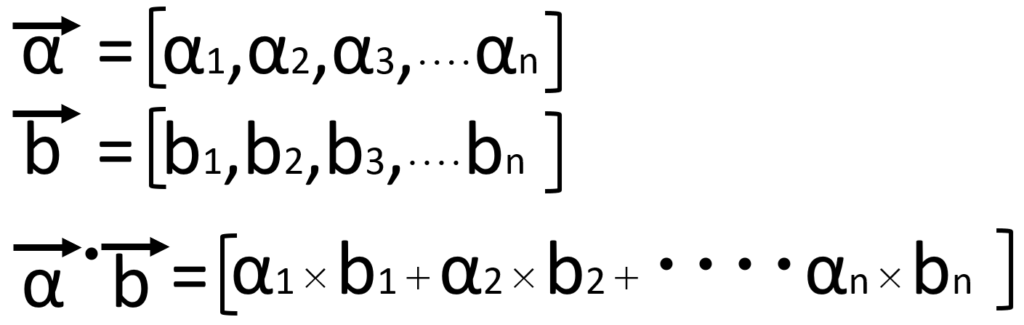
内積の意味は?
・ベクトル同士のなす角に関係がある
・内積が0なら「直交(垂直)」している
・機械学習のモデル(例:線形回帰)でも利用される
線形形式とベクトルの関係
線形形式(linear form)とは、変数に定数係数を掛けて足し合わせた式のことです。
二次元ベクトルの場合
ベクトル:(x, y)
線形形式:a₁x + a₂y(a₁, a₂は定数)
これは、ベクトル (x, y) と係数ベクトル (a₁, a₂) の内積でもあります。
→ a₁x + a₂y = (a₁, a₂)・(x, y)
n次元でも同様
ベクトル:(v₁, v₂, …, vn)
線形形式:a₁v₁ + a₂v₂ + … + anvn
= 係数ベクトルと元のベクトルの内積
実務での活用例
- 機械学習:線形回帰モデルの予測式は、係数ベクトルと説明変数ベクトルの内積
- 画像処理:ピクセルごとのベクトル演算
- 自然言語処理:単語ベクトル同士の内積で「類似度」を測る
まとめ:ベクトルの理解は、データ活用の第一歩
ベクトルは、複数の数値を一つにまとめて扱える便利な表現方法です。機械学習や統計分析、画像処理など多くの分野で基盤となる概念であり、以下のような活用が可能になります。
・数値データの構造的な把握:各要素の意味や関係性を見極めやすくなります。
・計算処理の効率化:内積やスカラー倍といった基本操作を通じて、複雑な処理もシンプルに実装できます。
・線形形式とのつながりを理解:ベクトルを内積で表すことで、データと係数(重み)によるモデル化の考え方にもつながります。
この記事では、ベクトルの定義から内積の計算、線形形式としての表現方法までを紹介しました。これらの基礎を押さえることで、今後のデータ分析やAI活用においても、より深い理解と応用が可能になります。



コメント