DS018:ピアソンの相関係数の分母と分子を説明できる
この記事で解決できる課題
・相関係数って何?よく聞くけど意味がよく分からない
・分母・分子の計算式を見ると混乱する
・データ分析で「相関を見ること」の本質を知りたい
この記事を読めば、「ピアソンの相関係数」がどんな意味を持つのか、数式を通して直感的に理解できるようになります。
ピアソンの相関係数とは?
ピアソンの相関係数とは、「2つの連続変数がどれだけ一緒に動いているか(線形的な関係)」を示す指標です。値の範囲は-1 ~ 1であり、それぞれ下記の意味となります。
1:完全な正の相関(片方が増えるともう一方も増える)
0:相関なし(関係性が見られない)
-1:完全な負の相関(片方が増えるともう一方は減る)
この相関係数は「r」と表記され、統計的には次のような式で定義されます。
数式で見る相関係数の構造
ピアソンの相関係数は以下のような式で定義されます。
この式を分解してみましょう。
分子:共分散(Covariance)
これは 共分散 です。
→「Xが平均より大きいとき、Yも平均より大きいことが多い」なら正の値に、
→「Xが大きいときにYは小さい」なら負の値になります。
つまり、2つの変数の“同時の動き”の方向性を表しています。
分母:標準偏差の積
これは、XとYそれぞれのばらつき(標準偏差)です。
→分母が大きいと「個別のばらつきが大きい」=相関係数の値は小さくなります。
→分母が小さいと「似た動き」でも相関が高くなりやすい。
ポイントまとめ:分母と分子の意味
| 部分 | 意味 | 直感的な理解 |
|---|---|---|
| 分子 | 共分散 | 2つの変数の「同じ方向への動き」 |
| 分母 | 標準偏差の積 | それぞれの変数のばらつきの大きさ |
| 相関係数r | 正規化された共分散 | -1~1で「動きの一致度合い」を示す |
よくある誤解:相関と因果の違い
「相関があるからといって、片方が原因とは限らない」という点も重要です。
-
アイスの売上と熱中症の件数には相関がありますが、どちらも「気温の上昇」が原因です。
→相関はあくまで“関係の強さ”であり、因果関係の証明にはなりません。
実務での活用例
・マーケティング:広告費と売上の相関を調べて予算配分を最適化
・品質管理:温度と不良率の相関を調べて生産条件を最適化
・人事分析:労働時間と満足度の相関を確認し働き方改革へ活用
まとめ
ピアソンの相関係数は、2つの連続変数の線形な関係性の強さと方向を示す指標です。
・分子:2つの変数が同じ方向に動くかどうか
・分母:それぞれの変数のばらつきを正規化
・結果:-1~1のスケールで相関の強さを示す
「相関の意味を理解すること」は、単なるスキル習得ではなく、データから本質を読み解く第一歩です。ぜひ実務でも活用してみてください。

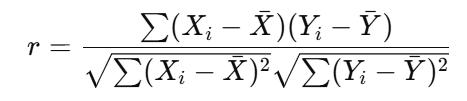
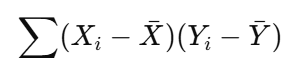
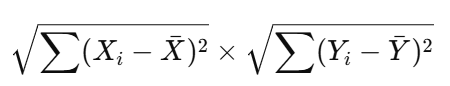


コメント