DS139:単回帰分析において最小二乗法、回帰係数、標準誤差、決定係数を理解し、モデルを構築できる
はじめに:この記事で解決できる課題
「単回帰分析を学びたいけど、どこから始めたらいいのかわからない」「回帰分析の用語が難しくて理解できない」という悩みを抱えていませんか?
単回帰分析は、ビジネス、研究、日常生活においてデータを分析し、予測や意思決定を行う際に役立つ強力な手法です。しかし、最小二乗法や決定係数といった専門用語が障壁となり、学習を挫折してしまうことも少なくありません。
この記事では、単回帰分析の基本的な概念と、その主要な要素(最小二乗法、回帰係数、標準誤差、決定係数)についてわかりやすく解説します。この記事を読むことで、単回帰分析の基礎を理解し、実践に役立てることができるようになります。
単回帰分析とは
単回帰分析は、1つの独立変数(説明変数)を使って1つの従属変数(目的変数)を予測するための統計手法です。
この手法の目的は、独立変数と従属変数の関係を直線で表現することです。回帰直線を用いることで、データの変動を理解したり、将来の値を予測したりすることができます。
例:
- 気温(独立変数)を使ってアイスクリームの売上(従属変数)を予測する
- 広告費(独立変数)から売上(従属変数)への影響を測定する
単回帰分析の主要な要素
1. 最小二乗法とは?
最小二乗法は、観測データと予測値の間の誤差の二乗和を最小化する方法です。この手法により、データに最も適合する回帰直線を計算します。
メリット:誤差が小さく、信頼性の高いモデルを構築できる。
例:実際の売上と予測売上の差(残差)が最も小さくなる直線を選ぶ。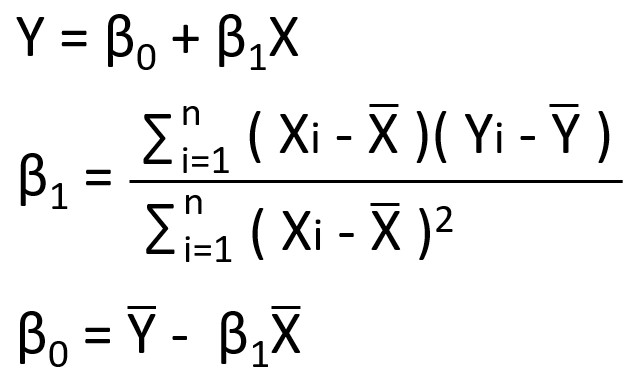
2. 回帰係数とは?
回帰係数は、独立変数が従属変数に与える影響の大きさを示します。例えば、広告費が1万円増加した場合、売上がどの程度変化するかを示します。
- ポイント:
- 正の値:独立変数が増加すると従属変数も増加。
- 負の値:独立変数が増加すると従属変数は減少。
3. 標準誤差とは?
標準誤差は、回帰係数の推定値のばらつきを示します。この値が小さいほど、回帰係数の信頼性が高いことを意味します。
- イメージ:
- 回帰直線の「精度のバロメーター」。
- 標準誤差が大きい場合、モデルがデータに適合していない可能性がある。

4. 決定係数(R²)とは?
決定係数は、モデルがデータのどれだけの変動を説明できるかを示す指標です。
- 数値の意味:
- 0に近い:モデルがデータをほとんど説明できていない。
- 1に近い:モデルがデータをほぼ完全に説明できる。
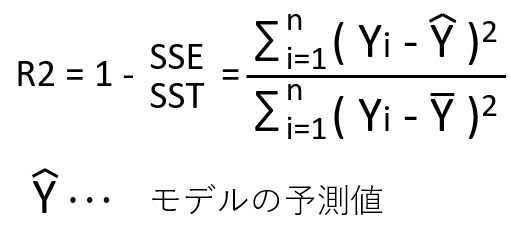
単回帰分析の活用例
単回帰分析は、以下のような場面で広く使われています。
1. ビジネス分析
- 広告費用が売上に与える影響を把握する
- 市場動向を予測して販売戦略を立案する
2. 学術研究
- 環境データを分析して気候変動の影響を測定する
- 健康データをもとに疾患のリスクを予測する
3. 日常生活
- 家計簿データから支出パターンを分析する
- 運動量が体重に与える影響を確認する
単回帰分析を使う際の注意点
-
独立変数と従属変数の関係が線形であることを確認する
- 線形の関係がない場合、他の手法(非線形回帰など)を検討すべきです。
-
外れ値(特異点)に注意する
- 外れ値がモデルに大きな影響を与える場合があります。
-
データの正規性を確認する
- データが正規分布に従っていない場合、結果の信頼性が低下することがあります。
まとめ:単回帰分析でデータの関係を明確にしよう
単回帰分析は、データから重要な洞察を得るための基本的な手法です。最小二乗法、回帰係数、標準誤差、決定係数といった要素を理解することで、データの背後にある関係性をより深く知ることができます。
この記事で紹介した内容を参考に、日々のデータ分析に単回帰分析を取り入れてみてください。


コメント