DS005:微分により計算する導関数が傾きを求めるための式であることを理解している
この記事で解決できる課題
「導関数ってなに?」「微分とどう違うの?」「数学が苦手だけど、グラフの傾きを知りたい」「極大点・極小点って何を意味しているの?」といった疑問に答えます。高校数学の復習にも、実務でグラフの変化を理解したい人にも役立つ内容です。
導関数とは?意味と役割
導関数とは、ある関数の「変化の仕方(傾き)」を表す新しい関数です。
例えば、関数f(x)=x²は、点によって変化の度合いが異なります。xが大きくなるほどグラフは急に上がります。こうした変化の度合い(=傾き)を数式で表したものが導関数です。
下図はf(x)を微分し、導関数f'(x)を求める式である。この式は「関数f(x)の微小な変化hに対する変化量」と解釈できます。この変化量は導関数の傾きとして現れ、変化が激しいと傾きは大きく、変化が緩やかなら傾きは小さくなります。
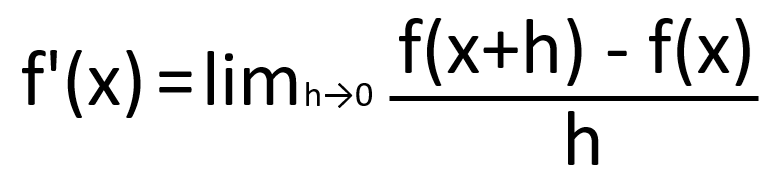
導関数はf'(x)以外にも下記のようにも表記される。
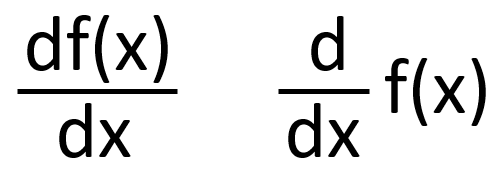
導関数を求める
では実際にf(x)=x^2の導関数を求めてみます。
まず最初に元になるf(x)を確認します。
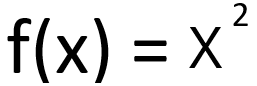
次に微小に変化させてf'(x)を確認します。
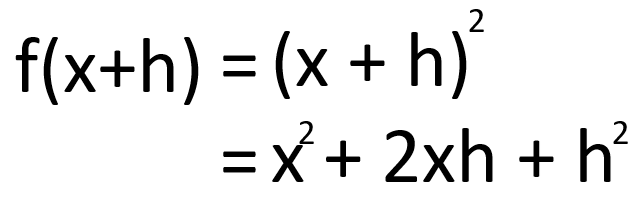
上記の2つの式を利用して微小に変化させる前後の差を求めます。
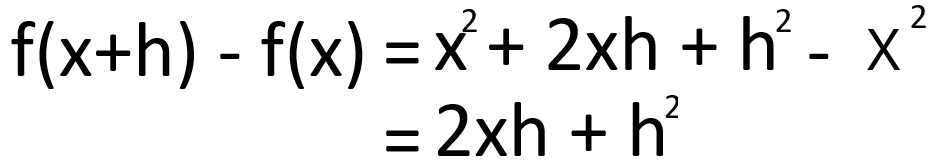
前後の差を変化させた値hで除算する事で単位あたりの変化量を求めます。
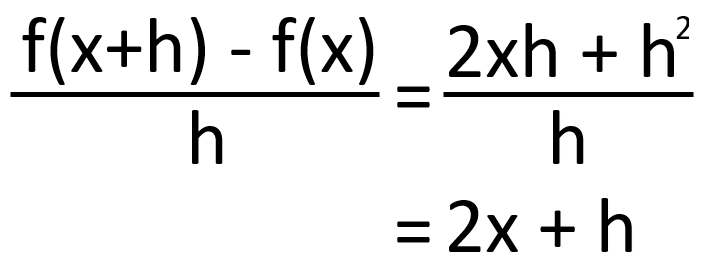
単位当たりの変化量に対してhを0に近づけたときの挙動を確認します。
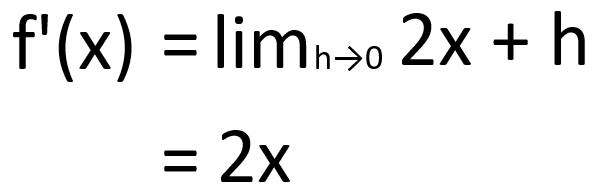
得られたF'(X)=2XからF(X)=x^2の各点の傾きを求める事が出来ます。x=1の時は「2」、x=2の時は「4」という具合です。
極大点と極小点
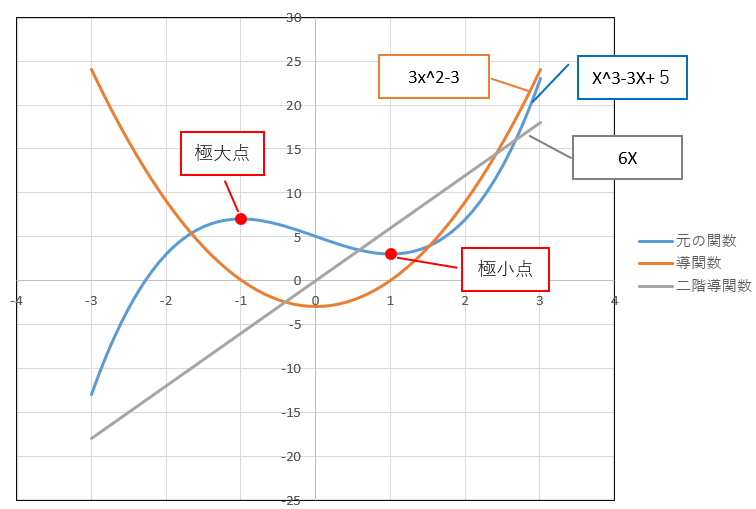
極大点と極小点の説明の前に二階導関数について説明します。二階導関数は関数f(x)から導いた導関数f'(x)をさらに微分した導関数f”(x)の事です。導関数f'(x)には関数f(x)の傾きを求める事が出来、二階導関数f”(x)は導関数f'(x)の変化率を求める事が出来ます。それを踏まえて下記の説明を行います。
極大点:関数が局所的に最大の値を取る点です。つまり、その点の近くで他の点よりも大きな値を取らないという性質を持ちます。下記の条件で見極めが出来ます。
- 導関数f'(x)のyが0である
- 二階導関数が負の値である(接線が右下がり)
極小点:極大点の逆です。
- 導関数f'(x)のyが0である
- 二階導関数が正の値である(接線が右上がり)
まとめ:導関数は「変化の見える化」
導関数は、関数の変化の速さを数値でとらえる道具です。
グラフの傾き=変化の度合いを知ることで、関数の特徴や挙動をより深く理解できます。
「関数がどう変わるか」を把握できるようになると、
問題解決の視点が一段と広がります。
導関数は、数学に限らずさまざまな分野で応用される“変化の視点”を与えてくれる考え方です。



コメント