順位相関係数とは？ピアソン・スピアマンの違いと使い分け

DS021：変数が量的、質的どちらの場合でも関係の強さを算出できる

データ分析では、変数同士の関係性を測ることが重要です。特に、データの種類によって適切な相関係数を選ぶことで、より正確な分析が可能になります。本記事では、ピアソンの積率相関とスピアマンの順位相関の違いを解説し、どのように使い分けるべきかを紹介します。

データの関係性を測る指標として、ピアソンの積率相関とスピアマンの順位相関があります。それぞれの特徴を比較すると以下のようになります。

相関係数	特徴	データの適用範囲
ピアソン相関	変数間の線形関係の強さを測る	量的データ（数値データ）
スピアマン相関	変数間の単調関係の強さを測る	順位データ・質的データ

単調関係とは、具体的な数値の増減の大きさには依存せず、「一方が増えれば他方も増える（単調増加）」「一方が増えれば他方は減る（単調減少）」という関係のことを指します。

ピアソン相関は線形関係を前提とするため、曲線的な関係には適しません。一方、スピアマン相関は順位に着目するため、非線形な関係でも相関を測ることができます。

以下の例を見てみましょう。

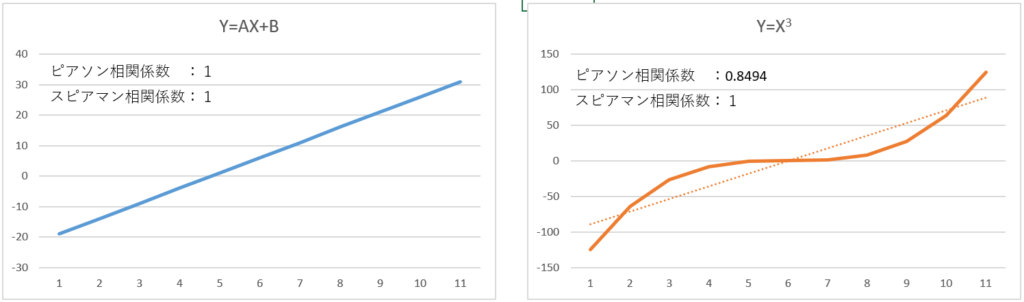
線形関係（Y = AX + B）
- ピアソン相関：1.0
- スピアマン相関：1.0
→ 完全な直線関係なので、どちらの相関係数も1になります。
非線形関係（Y = X³）
- ピアソン相関：1未満
- スピアマン相関：1.0
→ データはすべて単調増加しているため、スピアマン相関は1.0のままですが、ピアソン相関は曲線的な関係を考慮し1未満になります。